Riemannův tenzor křivosti
Tenzor křivosti ![]() popisuje křivost časoprostoru... K vysvětlení jeho významu si zavedeme následující pojem
popisuje křivost časoprostoru... K vysvětlení jeho významu si zavedeme následující pojem
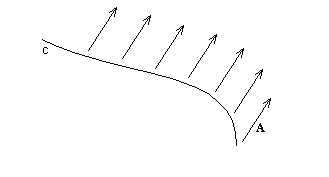
Paralelní přenos vektoru - je takový přenos, při kterém se daný vektor nemění (přibližně řečeno). Představme si nějakou libovolnou plochu a na ní nějakou křivku. Jestliže po této křivce paralelně přenášíme vektor, znamená to, že s vektorem míříme stále stejným směrem. Na tomto obrázku je vektor A paralelně přenášen podél křivky c:
 |
|
Pokud se takové přenosy odehrávají na ploše, je vše velice jednoduché a bez problémů. Zajímavěji to vypadá na křivých plochách, kde náhle zjistíme, že při paralelním přenosu mezi dvěma body záleží na tom, jakou cestu mezi nimi zvolíme - při použití různých cest (mezi týmiž dvěma body!) může vektor v cíli mířit pokaždé jinam, ačkoli byl vždy přenášen paralelně, tedy se s ním během cesty neotáčelo. To je důležitý poznatek o křivosti, který souvisí s Riemannovým tenzorem, jak si ukážeme... Zároveň je vidět, proč je takový problém porovnat vzájemné rychlosti vzdálených těles. V křivém prostoru je v každém místě jiná báze souřadné soustavy a abychom mohli porovnat dva vzdálené vektory, musíme je nejdřív paralelně přenést na jedno místo (do stejných souřadnic - viz afinní konexe). Protože však neexistuje pravidlo pro výběr cesty, po jaké máme za tímto účelem vektory tahat, moc jsme si paralelním přenosem nepomohli, když jeho výsledek je různý pro různé cesty. Rychlosti lze prostě porovnávat jenom v nějaké omezené oblasti, kde křivost ještě nepáchá tolik chaosu. Co se děje někde daleko, to už je věc tamní souřadné soustavy, se kterou ta naše nemá nic společného.
Jestliže provedeme paralelní přenos po uzavřené křivce (vrátíme se, odkud jsme vyšli), je zřejmé, že v plochém prostoru bude na konci cesty vektor mířit stejným směrem, jakým mířil na začátku. V zakřiveném však už může po návratu mířit jinam. Typický je příklad s povrchem koule, kde je věc snadno představitelná.
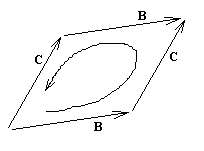
Tenzor křivosti pak vyjadřuje, jak se změní nějaký vektor, pokud s ním v daném prostoru provedeme paralelní přenos podél nějaké uzavřené křivky:

|
 je rozdíl mezi vektorem
je rozdíl mezi vektorem  před a po přenosu. Vektory
před a po přenosu. Vektory 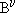 a
a  určují cestu, po které přenos uskutečníme a souvisí s délkou cesty (měla by být co nejmenší):
určují cestu, po které přenos uskutečníme a souvisí s délkou cesty (měla by být co nejmenší):
 |
|
Jak se daný vektor změní, to závisí také na volbě cesty (jaké zvolíme vektory 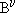 a
a  ). V plochém prostoru je Riemannův tenzor nulový, protože v něm paralelní přenos po uzavřených křivkách vektory nemění... Z tohoto pohledu je však nezakřivená například i válcová plocha, jelikož i na ní nemají tyto operace na vektory vliv. Plášť válce totiž vypadá křivě jenom zvenčí, tedy jakoby umístěn do prostoru o vyšším počtu rozměrů. V obecné relativitě si však nepředstavujeme, že časoprostor je v něčem umístěn, proto za křivost považujeme jenom to, co se jako křivost projevuje uvnitř tohoto časoprostoru. Pro obyvatele válcové plochy (nebo povrchu anuloidu) by jejich svět byl stejně dobře nezakřivený, jako prostá rovina. Teprve na povrchu koule by i oni zjistili, že je něco jinak - Riemannův tenzor je tedy nenulový jen tehdy, mohou-li si křivosti prostoru všimnout i jeho obyvatelé (jen v tom případě je totiž výsledkem nějaké působení - např. gravitace).
). V plochém prostoru je Riemannův tenzor nulový, protože v něm paralelní přenos po uzavřených křivkách vektory nemění... Z tohoto pohledu je však nezakřivená například i válcová plocha, jelikož i na ní nemají tyto operace na vektory vliv. Plášť válce totiž vypadá křivě jenom zvenčí, tedy jakoby umístěn do prostoru o vyšším počtu rozměrů. V obecné relativitě si však nepředstavujeme, že časoprostor je v něčem umístěn, proto za křivost považujeme jenom to, co se jako křivost projevuje uvnitř tohoto časoprostoru. Pro obyvatele válcové plochy (nebo povrchu anuloidu) by jejich svět byl stejně dobře nezakřivený, jako prostá rovina. Teprve na povrchu koule by i oni zjistili, že je něco jinak - Riemannův tenzor je tedy nenulový jen tehdy, mohou-li si křivosti prostoru všimnout i jeho obyvatelé (jen v tom případě je totiž výsledkem nějaké působení - např. gravitace).
Tenzor křivosti je antisymetrický v posledních dvou indexech:
|
což vlastně znamená, že pokud se vydáme při přenosu po cestě opačným směrem (výměna těchto indexů je jako výměna vektorů  a
a 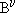 ), změní se vektor stejně, pouze s opačným znaménkem (v opačném směru)... Dále je cyklicky symetrický:
), změní se vektor stejně, pouze s opačným znaménkem (v opačném směru)... Dále je cyklicky symetrický:
|
a splňuje Bianciho identity:
|
Řekli jsme, že zakřivením prostoru vysvětlujeme gravitaci a zrychlení. Jelikož Riemannův tenzor popisuje právě ono zakřivení, měl by tím popisovat i gravitační účinky. Abychom ukázali, jak toto zajišťuje, vysvětlíme si nejdříve, co je to deviace a fokusace geodetik: mějme dvě geodetiky (nejkratší cesty v daném prostoru, přesněji křivky, které paralelně přenáší svůj vlastní tečný vektor). Tyto geodetiky ať jsou na začátku rovnoběžné. V plochém prostoru je to běžný případ rovnoběžných přímek, které jsou rovnoběžné stále. Když však přejdeme například na povrch koule, je jasné, že původně rovnoběžné "přímky" se zanedlouho protnou, i když jsou stále geodetické (tedy nikam neuhýbají). V případě sedlové plochy se naopak původně rovnoběžné geodetiky začnou odchylovat a vzdalovat. Toto nazýváme deviací a fokusací geodetik a je jasné, že rychlost vzájemného vzdalování či přibližování je úměrná křivosti a lze ji tedy určit pomocí Riemannova tenzoru:
|
což je rovnice deviace geodetik. Vektor Tν je tečný vektor geodetiky a Sσ je vektor, ukazující k sousední geodetice (spojuje místa se stejnou hodnotou afinního parametru); aμ je vzájemné zrychlení, čili druhá derivace vektoru Sσ. V obecné relativitě se říká, že tělesa se přirozeně pohybují po geodetikách. Pokud je však v nějakém místě přirozené, aby se dvě původně rovnoběžné dráhy začaly přiklánět k sobě a nakonec se protnuly (díky zakřivení), pak jsme objevili gravitaci, která dělá právě tohle.
