Ke speciální relativitě
Zde jsou uvedeny matematické vztahy pro transformace ve speciální relativitě:
| Lorentzova transformace |
| Dilatace času |
| Kontrakce délek |
| Skládání rychlostí |
| Relativistická hmotnost (opuštěný koncept) |
| Vztah hmotnosti a energie |
| Prostoročasové intervaly |
| Řešení zrychlených pohybů |
Postuláty speciální relativity
- Všechny inerciální vztažné soustavy jsou rovnocenné.
- Rychlost světla je stejná ve všech inerciálních soustavách.
Odvození Lorentzovy transformace
Chceme najít vztah mezi prostorovými a časovými souřadnicemi dvou inerciálních systémů (systémů bez zrychlení). Zvolíme si osové trojhrany tak, aby osy x obou soustav splývaly a osy y, z byly rovnoběžné. Soustava označená čárkou se pohybuje rovnoměrně přímočaře vzhledem k nečárkované soustavě rychlostí v:
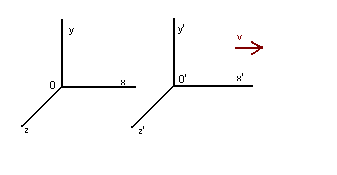
V čase t = 0 splývají oba počátky (0 = 0'). Hledaná transformace musí být lineární, aby z inerciálního systému vytvořila opět inerciální systém:
| x' = γx + δt |
| t' = αx + βt |
Musíme najít hodnoty koeficientů γ, δ: v obecném časovém okamžiku má počátek čárkované souřadné soustavy (x' = 0) v nečárkované souřadnici x = vt:
| 0 = γvt + δt ... z čehož plyne: δ = -γv |
| Dosadíme: x' = γx - γvt, čili x' = γ(x - vt) |
- Postulát požaduje rovnocennost obou systémů, tedy rychlost v obou systémech se může lišit maximálně znaménkem:
x' = γ(x - vt), x = γ(x' + vt') Dosadíme jednu rovnici do druhé: x = γ(γ(x - vt) + vt') ... upravíme: x = xγ2 - vtγ2 + γvt' ... vyjádříme t': t' = x/(γv) - γx/v + γt ...což upravíme na: t' = x(1 - γ2)/(γv) + γt - Postulát požaduje konstantnost rychlosti světla, čili signál vyslaný v čase t = 0 z počátku souřadnic je v čase t = x/c (c je rychlost světla ve vakuu) v místě, pro které platí:
| x' = γ(x - vt) ... a zároveň x' = ct', tedy: |
| ct' = γ(c - v)t ... protože x = ct a čas t jsme vytkli |
| Do tohoto vztahu dosadíme ... |
| za t' = t(c(1 - γ2)/(γv) + γ) a dostaneme: |
| ct(c(1 - γ2)/(γv) + γ) = γ(c - v)t ... |
| čas t se zkrátí a můžeme vyjádřit γ ... |
| γ = 1/(1 - v2/c2)1/2 |
Čili Lorentzova transformace je:
| x' = (x - vt)/(1 - v2/c2)1/2 |
| t' = (t - xv/c2)/(1 - v2/c2)1/2 |
| y' = y, z' = z |
Z této transformace lze odvodit všechny následující vztahy.
Dilatace času
Vyplývá z následujíchích výrazů
| t0 = t'2 - t'1 t = t2 - t1 |
 |
Jestliže někdo změří, že mezi dvěma událostmi, které nastaly na tomtéž místě, uplynulo t0 sekund, potom jiný pozorovatel, který se vzhledem k prvnímu pohybuje rychlostí v, změří t sekund mezi oběma událostmi. Vždy bude t >= t0 (pokud obě události nastanou na tomtéž místě). Například mezi dvěma záblesky (na stejném místě) uplynulo pro člověka v klidu jedna sekunda, ale letí-li někdo kolem rychlostí 280 000 km/s, trvá to pro něj 2 sekundy a 78 setin. Pro rychlosti "malé" (třeba i tisíc km za sekundu!) je rozdíl neznatelný.
Pro nesoumístné události (na různých místech) tento vztah neplatí, protože se uplatňuje relativnost současnosti, která může zásadně změnit poměry ve studované situaci.
Kontrakce délek
Vzplývá z
| L0 = x2' - x1' |
 |
L0 je pro pozorovatele v klidu, délku L vidí pozorovatel o rychlosti v, která je přesně ve směru délky L. Vždy platí, že L0 >= L. Vidí-li tedy někdo tyč délky 4 metry, pak pro někoho o rychlosti 216 000 km/s a směru rovnoběžném s tyčí má délku 2 metry a 77 centimetrů.
Skládání rychlostí
Odvozuje se pomocí vztahů:
| u = dx/dt, u' = dx'/dt' |
 |
Rychlosti u, v musí být rovnoběžné. Je-li v jisté soustavě rychlost nějakého tělesa rovna u', potom v soustavě o rychlosti v vzhledem k té první se rychlost tělesa jeví jako u. Například kolem nás někdo letí rychlostí 240 000 km/s a vyšle před sebe projektil rychlostí 210 000 km/s (vzhledem k sobě). My zjistíme rychlost projektilu 288 461 km/s. Zvolíme-li u' jako rychlost světla, vyjde nám u opět rychlost světla pro jakoukoli rychlost v... Chceme-li transformaci zobecnit na libovolný směr rychlosti u, získáme následující vztahy pro jednotlivé složky (rychlost v však musí mít stále směr osy x):
 |
 |
 |
Relativistická hmotnost
Relativistická hmotnost je opuštěný koncept, protože neplní v teorii žádnou úlohu (nevystupuje v žádných dalších rovnicích). Jedná se vlastně o celkovou energii dělenou čtvercem rychlosti světla, jde tedy o veličinu nadbytečnou, když ji lze vyjádřit jako veličinu jinou. A zatímco celková energie je přímo měřitelná, u relativistické hmotnosti by přímé měření byl problém. Navíc by výsledek měření závisel na směru, kterým bychom na těleso při měření silově působili. Proto se tento pojem v teorii relativity nepoužívá, pod pojmem hmotnost se rozumí pouze hmotnost klidová a zde je krátký odstavec o relativistické hmotnosti uveden jen z historických důvodů.
Jelikož se hmotnost projevuje při dynamických dějích (srážky apod.), odvozuje se vztah pro relativistickou hmotnost ze zákona zachování hybnosti:
| m1u1 + m2u2 = (m1 + m2)v |
m1, m2 jsou hmotnosti dvou objektů, které se srazí, u1 a u2 jsou jejich rychlosti před srážkou, v je rychlost po srážce. Uplatní se pravidlo o skládání rychlostí, které vlastně způsobí i relativistickou "změnu hmotnosti":
 |
V klidové soustavě má těleso hmotnost m0, v soustavě o rychlosti v se jeví, že má (setrvačnou) hmotnost m. Je vždy m >= m0. Transformace se týká pouze setrvačné hmotnosti, jelikož pouze ta hraje roli při výměně hybnosti. Prvotním jevem je zde dilatace času, díky které je snaha o další urychlení letícího tělesa stále méně účinná, jako by těleso mělo stále vyšší hmotnost. To ovšem platí pouze ve směru pohybu tělesa, nikoli ve směru kolmém. U klidové hmotnosti na směru působení síly nezáleží, takže relativistická hmotnost se chová abnormálně. Relativistickou hmotnost také nelze použít pro výpočet gravitačních účinků. V obecné teorii relativity se gravitační účinky pohybujících se těles počítají jiným způsobem - pomocí energie a hybnosti (nikoli pomocí hmotnosti). Jak už bylo řečeno, nehraje relativistická hmotnost v teorii relativity žádnou užitečnou roli. Namísto ní se používá celková energie tělesa, která zahrnuje jak klidovou energii, tak i kinetickou energii. Pod pojmem hmotnost se tedy vždy rozumí klidová hmotnost, která je stejná ve všech soustavách.
Vztah hmotnosti a energie
Z výrazu pro relativistickou hmotnost plyne, že
| m2(c2 - v2) = m02.c2 |
Po diferencování obdržíme
| 2m(c2 - v2)dm - m22v.dv = 0 |
což upravíme na
| mv.dv + v2.dm = c2dm (1) |
Pro energii platí
| dE = F.ds = ds.d(m.v)/dt = v.d(m.v) |
| = v2.dm + mv.dv (2) |
Porovnáním obou výsledků (1, 2) získáme vztah
| dE = c2 dm |
Z toho plyne:
| E = mc2 |
což je známý Einsteinův vztah mezi hmotností a energií. Říká se v něm, že hmotnosti m odpovídá energie E (konstantou úměry je c2 = 9.1016 m2.s-2). Na první pohled vychází i pro malé hmotnosti obrovská energie - už pro jeden kilogram je to 9.1016 Joulů. Tolik energie ve formě fotonů bychom získali z libovolného tělesa o hmotnosti jeden kilogram jeho úplnou přeměnou na záření. Běžné metody získávání energie jsou tedy velmi neúčinné.
Prostoročasové intervaly
Vzdálenost mezi dvěma událostmi v trojrozměrném prostoru určíme snadno pomocí Pythagorovy věty:
| s2 = x2 + y2 + z2 |
Tato vzdálenost se nezmění, ani když přejdeme do jiné souřadné soustavy (posunuté, pootočené, atd). Nemění se ani pod vlivem Galileiho transformace. V různých souřadných soustavách mohou být různě velké jednotlivé složky vzdálenosti (x, y, z), ale celková délka je vždy stejná. Například vzdálenost židle od stolu je vždy 7 metrů, ať už použijeme soustavu, kde jednotlivé složky jsou (2, 3, 6), nebo jinou soustavu, kde složky jsou (3, 6, 2). Složky se mohou měnit, protože ty jen souvisí s volbou souřadnic. To však nemá vliv na délku jako takovou. V teorii relativity je to ovšem trochu jinak: židle od stolu může být různě daleko z pohledu různých soustav ve vzájemném pohybu (kontrakce délek), takže pouhá prostorová vzdálenost už není neměnná při přechodu do jiné soustavy. Pokud chceme i v teorii relativity najít jakousi vzdálenost mezi dvěma body, která nezávisí na volbě souřadné soustavy, musíme do ní zahrnout i čas. Je to proto, že v teorii relativity nejsou čas a prostor odděleny, ale sloučeny do jedné entity - časoprostoru, kde se do jisté míry mohou pro různé pozorovatele čas i prostor mísit. Pokud se z pohledu jedné soustavy kontrahuje nějaká délka, pak se zároveň mění i časové intervaly. Tyto 2 efekty jdou v časoprostoru proti sobě. To, co se nemění, se nazývá časoprostorový interval, čili jakási "vzdálenost" mezi body v časoprostoru:
| s2 = x2 + y2 + z2 - c2t2 |
Podobně jako v předchozím případě - dvě události mohou mít v různých soustavách různé složky časoprostorového intervalu: mohou být sobě blíž (kontrakce délek), může mezi nimi být jiný časový odstup (relativnost současnosti). Ale časoprostorový interval je pro danou dvojici událostí vždy stejný, ať už zvolíme jakoukoli inerciální soustavu. Prostorová vzdálenost nebo časový interval jsou jen složky, které se mohou měnit podle volby vztažné soustavy. To však nemá vliv na časoprostorový interval jako takový. Je to důležitý aspekt teorie relativity: jsou tu jisté veličiny, které relativní nejsou. Ty se nazývají invarianty a jsou to vlastně pozorovatelné veličiny. Příkladem invariantu je kromě časoprostorového intervalu například i vlastní čas, čtyřrychlost, čtyřhybnost, atd. Tyto veličiny jsou stejné pro všechny pozorovatele a nemění se při přechodu k jiné souřadné soustavě. Hrají tedy v teorii relativity důležitou úlohu a Einstein chtěl původně svou teorii nazvat teorií invariantů.
Proč však má čas opačné znaménko a navíc je násoben rychlostí světla? V časoprostoru je žádoucí, aby jednotky na všech 4 osách byly stejné. Prostorové osy mají jednotku délkovou (například metr), ovšem časová osa by měla jednotku časovou (například sekunda). Čas je možné převést na délku vynásobením rychlostí. K tomu se rychlost světla ve vakuu sama nabízí, protože je neměnná.
A teď klíčová otázka: záporné znaménko u času. To popisuje důležitou vlastnost časoprostoru, díky které má světlo stejnou rychlost ve všech vztažných soustavách. Kdyby tam bylo kladné znaménko, pak by se takto definovaný interval měnil při Lorentzově transformaci. Takto definovaný interval by byl neměnný pouze v nerelativistickém čtyřrozměrném časoprostoru, který nevykazuje žádnou kontrakci délek ani relativnost současnosti a světlo tam lze dohonit. Prohozením znaménka u času zajistíme, že se takto definovaný časoprostor chová v souladu s experimenty. Tento časoprostor se nazývá Minkowského časoprostor a díky zápornému znaménku u času jeho geometrie není Euklidovská, ale hyperbolická.
Všimněme si, že pro s=0 lze výraz upravit na tvar
| c2t2 = x2 + y2 + z2 |
To je rovnice koule, která se v čase zvětšuje rychlostí světla. Může tedy představovat světelný záblesk, šířící se od středu na všechny strany. Rychlost světla je však vždy stejná, proto i tato "zvětšující se koule" vypadá stejně pro všechny pozorovatele: pokud například někdo vyslal onen záblesk právě v okamžiku, kdy ho míjel letící pozorovatel, pak oba jsou ze svého pohledu stále uprostřed narůstající sféry, i když jsou ve vzájemném pohybu. Z toho je vidět, že čas obou nemůže být stejný. Pak by totiž světelná koule musela mít dva různé středy.
Představme si, že ve směru letu pohybujícího se pozorovatele je na jednom místě značka. Řekněme, že stojící pozorovatel změří, že čelo světelné koule dopadlo na značku sekundu po záblesku (značka je v jeho soustavě tedy 300 tisíc kilometrů daleko). Stojící pozorovatel spočítá, že prostoročasová vzdálenost mezi zábleskem a dopadem světla na značku je nulová. Letící pozorovatel má danou prostorovou vzdálenost kontrahovanou. Čas, který v jeho soustavě uplyne mezi zábleskem a dopadem světla na značku, je také zkrácený (zde nelze použít dilataci času, protože jde o nesoumístné události a uplatňuje se tedy relativnost současnosti). Prostorový i časový odstup v jeho soustavě jsou zkráceny právě tak, že i jemu vyjde prostoročasový interval mezi těmito událostmi nulový. Je vidět, že oddělené časové a prostorové vzdálenosti jsou sice relativní, ale kombinovaná prostoročasová vzdálenost už relativní není.
Řešení zrychlených pohybů
Speciální teorie relativity sice vychází z vlastností inerciálních (nezrychlených) soustav, to jí však nebrání počítat i zrychlené pohyby (ovšem pouze vztažené k inerciálním soustavám). Postupujeme tak, že obecný pohyb rozdělíme na velmi krátké úseky. S každým takovým úsekem lze spojit lokální inerciální soustavu díky jeho omezené délce. Vyřešíme pohyb v každé takové části a výsledky potom sečteme. To je samozřejmě postup šitý na míru diferenciálnímu a integrálnímu počtu. Zde je například vztah pro vlastní čas pozorovatele, pohybujícího se v časoprostoru po světočáře, zadané parametricky jako xμ = xμ(λ):
 |
Zde ημν = diag(-c2,1,1,1) je metrika plochého prostoru. Vlastní čas Δτ je čas, který daný pozorovatel sám naměří hodinkami, které si nese s sebou. Světočára (dráha pozorovatele v časoprostoru) nesmí nikde překročit rychlost světla. Pokud tento postup použijeme na známý paradox dvojčat a spočítáme vlastní čas na Zemi a vlastní čas v raketě putující "tam a zase zpátky", skutečně nám vyjde, že na Zemi uplyne více času (pro cestovatele je možné použít libovolnou světočáru časového typu). Tento postup však nebere v úvahu gravitaci a neinerciální síly, lze ho tedy použít pouze při popisu pohybu z hlediska ineciální soustavy - tedy například z pohledu Země. Už takto nelze spočítat pohyb z hlediska cestujícího pozorovatele, protože ten pociťuje účinek neinerciálních sil: při obratu brzdí a zrychluje na zpáteční cestu. Pro něj je potřeba použít obecnou teorii relativity.
